훈련된 분류 모델의 품질 평가
1. 이진 분류기의 예측 평가하기 : Confusion Metrix을 통한 교차검증
(이진분류 : 0,1 로 분류하는 로지스틱 회귀)
- TP : 진짜 양성 개수, 양성 클래스중에서 올바르게 예측한 샘플 개수
- TN : 진짜 음성 개수, 음성 클래스 중에서 올바르게 예측한 샘플 개수
- FP : 거짓 양성 개수, 1종 에러라고 부르고, 양성 클래스로 예측한 것 중에서 실제 음성 클래스인 샘플 개수
- FN : 거짓 음성 개수, 2종 에러라고 부르고, 음성 클래스로 예측한 것 중에서 실제 양성 클래스인 샘플 개수
사이킷런 cross_val_score
교차검증을 수행할 때 scoring 매개변수에 성능 지표 중 하나를 선택할 수 있다.
정확도, 정밀도, 재현율, F₁이 있다. 이 중 정확도는 많이 사용되는 성능 지표이고 단순하게 올바르게 예측된 샘플의 비율로 보면 된다.
# 라이브러리 임포트
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
# 특성 행렬과 타깃 벡터 생성
X,y = make_classification(n_samples=10000,
n_features=3,
n_informative=3,
n_redundant=0,
n_classes=2,
random_state=1)
# 로지스틱 회귀 모델 생성
logit = LogisticRegression()
cross_val_score(scoring="accuracy")
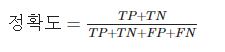
기본값인 3-폴드 교차검증의 정확도를 측정할 수 있다.
# 정확도를 사용한 교차검증 수행
cross_val_score(logit, X, y, scoring="accuracy")
array([0.9555, 0.95 , 0.9585, 0.9555, 0.956 ])정확도는 직관적이고 쉽게 설명할 수 있다는 장점이 있다. 정확도는 단순히 정확히 예측한 샘플의 비율로 실전에선 클래스 비율이 불균형한 데이터가 많다.
예를 들면 샘플의 99.9%는 클래스 1이고 0.1%만이 클래스 2인 경우이다.
클래스가 이렇게 불균형하면 모델의 정확도는 높고, 예측 성능이 나쁜 역설적인 상황이 발생한다.
또 예를 들자면 전체 인구 0.1%에서 발생하는 매우 희귀한 암의 발병을 예측한다면, 어떤 모델 훈련 후 95%의 정확도를 얻는다. 하지만 0.1%를 제외한 99.9%의 사람들이 암에 걸리지 않으므로 단순히 아무도 암에 걸리지 않았다고 예측하는 모델을 만들면 4.9%만큼 더 정확한 모델을 만들 수 있다.
이런 이유 때문에 정밀도, 재현율, F₁점수 같은 다른 지표도 사용된다.
cross_val_score(scoring="precision")
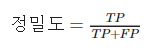
정밀도는 양성으로 예측한 샘플 중에서 진짜 양성 클래스의 비율이다. 이를 예측에 포함된 잡음이라 생각할 수 있다.
높은 정밀도의 모델은 양성 클래스라고 확신이 높을 때만 양성 샘플로 예측한다.
# 정밀도를 사용한 교차검증
cross_val_score(logit, X, y, scoring="precision")
array([0.95963673, 0.94820717, 0.9635996 , 0.96149949, 0.96060606])cross_val_score(scoring="recall")
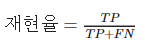
재현율은 진짜 양성 샘플 중에서 양성으로 예측한 비율로, 모델이 양성 클래스 샘플을 구분하는 능력을 측정한다. 높은 재현율의 모델은 샘플을 양성 클래스로 예측하기 위해서 낮은 기준을 가진다.
# 재현율을 사용한 교차검증
cross_val_score(logit, X, y, scoring="recall")
array([0.951, 0.952, 0.953, 0.949, 0.951])cross_val_score(scoring="f1")

정밀도와 재현율은 이해하기에 덜 직관적이다. 항상 정밀도와 재현율 간의 균형을 맞추어야 한다. 그러기 위해 F₁점수가 만들어졌다. F₁은 정밀도와 재현율의 조화평균을 나타낸다. (비율에 대한 평균의 한 종 류)
이는 진짜 양성 레이블을 가진 샘플을 양성을 성공적으로 예측한 정도를 측정한다.
# f1 점수를 사용한 교차검증
cross_val_score(logit, X, y, scoring="f1")
array([0.95529884, 0.9500998 , 0.95827049, 0.95520886, 0.95577889])평가 지표로서 정확도는 유용한 성질을 가지고 있다. 특히 이해하기가 쉽다. 그러나 종종 정밀도와 재현율의 균형을 맞추는것이 더 좋은 지표가 된다.
F₁점수는 정밀도와 재현율을 비교적 동등하게 취급하여 이 둘 사이의 균형을 표현한다.
cross_val_score를 사용하는 대신
진짜 y값과 예측한 y값이 있으면 직접 정확도와 재현율을 계산할 수 있다.
# 라이브러리 임포트
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 훈련세트와 테스트세트 분할
X_train, X_test, y_train, y_test = train_test_split(X,
y,
test_size=0.1,
random_state=1)
# 테스트 세트의 예측 만들기
y_hat = logit.fit(X_train, y_train).predict(X_test)
# 정확도 계산 (종속변수의 시험셋, 종속변수의 예측 값)
accuracy_score(y_test, y_hat)
0.947#cross_val_score
cv 매개변수를 지정하지 않으면 회귀일 때는 KFold, 분류일때는 StratifiedKFold 분할기가 사용된다. cv 매개변수에 정수를 입력하여 기본 분할기의 폴드 수를 지정할 수 있다.
#cross_validate
이함수는 cross_val_score 함수와 비슷하지만 scoring 매개변수에 여러 개의 평가 지표를 추가할 수 있다.
from sklearn.model_selection import cross_validate
# 정확도와 정밀고를 사용한 교차검증
cross_validate(logit, X, y, scoring=["accuracy", "precision", "recall", "f1"])
{'fit_time': array([0.0215714 , 0.021487 , 0.02097559, 0.02140188, 0.05238557]),
'score_time': array([0.00853634, 0.00787544, 0.00747252, 0.00705051, 0.00703382]),
'test_accuracy': array([0.9555, 0.95 , 0.9585, 0.9555, 0.956 ]),
'test_precision': array([0.95963673, 0.94820717, 0.9635996 , 0.96149949, 0.96060606]),
'test_recall': array([0.951, 0.952, 0.953, 0.949, 0.951]),
'test_f1': array([0.95529884, 0.9500998 , 0.95827049, 0.95520886, 0.95577889])}이진 분류기를 여러가지 확률 임곗값으로 평가
분류 문제는 예측 결괏값이 비연속적인 경우이다. 예와 아니오 처럼 답변을 얻게 된다. 이때 얻을 수 있는 분류 종류를 클래스라고 부른다. 클래스가 2개뿐일 때 이진분류라고 한다.
2. 이진 분류기 임곗값 평가하기 : ROC 곡선
이진 분류기를 여러 가지 확률 임곗값으로 평가한다.
ROC 곡선은 이진 분류기의 품질을 평가하는데 널리 사용하는 방법이다. ROC는 확률 임곗값(어떤 샘플을 한 클래스로 예측할 확률)마다 진짜 양성과 거짓 양성 개수를 비교한다.
ROC 곡선을 그리면 모델의 성능을 확인할 수 있다. 모든 샘플을 올바르게 예측하는 분류기는 수직으로 꼭대기까지 올라간다. 랜덤하게 예측하는 분류기는 대각선으로 나타난다. 좋은 모델일수록 수직으로 꼭대기까지 올라가는 선에 가깝다.
roc_curve로 사용하여 임곗값마다 진짜 양성과 거짓 양성을 계산하여 그래프를 그릴 수 있다.
# 라이브러리 임포트
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, roc_auc_score
from sklearn.model_selection import train_test_split
# 특성 행렬과 타깃 벡터 생성
features, target = make_classification(n_samples=10000,
n_features=10,
n_classes=2,
n_informative=3,
random_state=3)
# 훈련세트와 테스트세트 분할
features_train, features_test, target_train, target_test = train_test_split(features, target, test_size=0.1, random_state=1)
# 로지스틱회귀 분류기 생성
logit = LogisticRegression()
# 모델 훈련(학습)
logit.fit(features_train,target_train)
LogisticRegression()# 특성(x)세트 일부로 목표변수에 대한 예측 확률 계산
target_probabilities = logit.predict_proba(features_test)[:,1]
# 테스트셋으로 진짜 양성 비율과 거짓 양성 비율 계산
false_positive_rate, true_positive_rate, threhold = roc_curve(target_test, target_probabilities)
# ROC 곡선 그리기
plt.title("Receiver Operating Characteristic")
plt.plot(false_positive_rate, true_positive_rate)
plt.plot([0,1], ls="--")
plt.plot([0,0], [1,0], c=".7"), plt.plot([1,1], c=".7")
plt.ylabel("True Positive Rate")
plt.xlabel("Fale Positive Rate")
plt.show()
이전까지 예측값 기반 모델 평가를 했다. 머신러닝 알고리즘들은 확률을 기반으로 예측값을 만든다. 즉 모든 샘플은 각 클래스에 속할 명시적인 확률이 주어진다. predict_proba 메소드를 사용해 해결에 있는 첫 번째 샘플에 대한 예측확률을 확인할 수 있다.
# 예측 확률 계산
logit.predict_proba(features_test)[0:1]
array([[0.86891533, 0.13108467]])# classes_ 로 클래스 확인
logit.classes_
array([0, 1])첫 번째 샘플은 음성 클래스(0)가 될 가능성이 87% 정도, 양성 클래스(1)가 될 가능성이 13%이다. 기본적으로 사이킷런은 확률이 0.5(임곗값) = 50% 보다 크면 양성 클래스로 예측된다.
실제 필요에 의해 중간값보다 다른 임곗값을 사용해 모델을 편향되게 만들어야 할 때가 있다. 예를 들면 거짓 양성이 회사에 매우 큰 비용을 치르게 한다면 확률 임곗값이 높은 모델을 선호한다.
일부 양성 샘플을 예측하지 못할 수 있지만 양성으로 예측된 샘플은 이 예측이 맞을 것이라고 강하게 확신할 수 있다. 이것은 진짜 양성비율(TPR)과 거짓 양성비율(FPR) 사이의 트레이드오프이다.
진짜 양성 비율은 올바르게 예측된 양성 샘플 개수를 전체 진짜 양성 샘플의 수로 나눈 것이다.
거짓 양성 비율은 잘못 예측된 양성 클래스 개수를 모든 진짜 음성 클래스 샘플수로 나눈 것이다.
print("임곗값:", threhold[116])
print("진짜 양성 비율:", true_positive_rate[116])
print("거짓 양성 비율:", false_positive_rate[116])
임곗값: 0.5331715230155316
진짜 양성 비율: 0.810204081632653
거짓 양성 비율: 0.14901960784313725
→ ROC 곡선은 확률 임곗값마다 TPR(진짜 양성비율)과 FPR(거짓 양성비율)을 나타낸다.
여기선 임곗값이 0.5일 때 TPR 0.81 이고, FPR는 0.15이다.
print("임곗값:", threhold[45])
print("진짜 양성 비율:", true_positive_rate[45])
print("거짓 양성 비율:", false_positive_rate[45])
임곗값: 0.8189133876659292
진짜 양성 비율: 0.5448979591836735
거짓 양성 비율: 0.047058823529411764
→ 임곗값을 80%로 증가시키면(샘플을 양성으로 예측하기 위해 모델이 확신하는 정도를 증가) TPR과 FPR이 크게 감소한다.
낮은 TPR이 나온 이유는 양성 클래스로 예측하기 위한 기준을 높였기 때문에 모델이 많은 양성 샘플을 구분하지 못한것이다.
또한 낮은 FPR의 이유는 양성 클래스로 예측되는 음성 샘플의 수를 감소시킨것이다.
TPR과 FPR간의 트레이드오프를 시각화하는 것 외에 ROC 곡선은 일반적인 모델 지표로 사용할수도 있다.
ROC 곡선 아래 면적(AUCROC) : roc_auc_score
좋은 모델일수록 곡선이 위로 올라가고, 곡선 아래 면적이 커지게된다. 이런 이유에서 ROC 곡선 아래 면적(AUCROC)을 계산해 모든 가능한 임곗값에서 모델의 전반적인 품질을 평가한다.
AUROC가 1에 가까울수록 더 좋은 모델이다. 사이킷런에서는 roc_auc_score 함수를 사용하여 계산할 수 있다.
# ROC 곡선 아래 면적 계산 : # 종속변수 시험셋, 특성(x)세트 일부로 목표변수에 대한 예측 확률 계산된 값
roc_auc_score(target_test, target_probabilities)
0.9073389355742297정밀도-재현율 곡선 - precision_recall_curve
TPR(진짜 양성비율) 재현율의 다른 이름이다. ROC 곡선 외에 정밀도와 재현율을 사용한 정밀도-재현율 곡선을 그려 모델을 평가 할 수 있다.
이 함수는 임계점마다 정밀도와 재현율을 계산해 정밀도-재현율 곡선을 그린다.
정밀도 = 양성으로 예측한 샘플 중에서 진짜 양성 클래스의 비율
재현율 = 진짜 양성 샘플 중에서 양성으로 예측한 비율
from sklearn.metrics import precision_recall_curve
# 진짜 양성비율 TPR과 거짓 양성비율 FPR 계산
precision, recall, threhold = precision_recall_curve(target_test, target_probabilities)
# ROC 곡선 그리기
plt.title("Precision-Recall Curve")
plt.plot(precision, recall)
plt.plot([0,1], ls="--")
plt.plot([1,1], c=".7"), plt.plot([1,1],[1,0], c=".7")
plt.ylabel("Precision")
plt.xlabel("Recall")
plt.show()
정밀도-재현율 곡선에서는 오른쪽 맨 위에 가까울수록 좋은 모델이다.
여기서 아래 면적을 평균 정밀도라 부르고, 평균 정밀도는 average_precision_score 함수를 사용해 계산할 수 있다.
from sklearn.metrics import average_precision_score
# 평균 정밀도 계산
average_precision_score(target_test, target_probabilities)
0.8984128719848977교차검증 함수의 scoring 매개변수에 ROCAUC와 평균 정밀도를 평가 지표로 지정할 수도 있다.
cross_validate(logit, features, target, scoring=["roc_auc", "average_precision"])
{'fit_time': array([0.06238627, 0.05151367, 0.0444777 , 0.03644228, 0.0467484 ]),
'score_time': array([0.01094103, 0.00890207, 0.0094552 , 0.00484657, 0.01493096]),
'test_roc_auc': array([0.9007689, 0.918251 , 0.90882 , 0.915359 , 0.90261 ]),
'test_average_precision': array([0.90028629, 0.90967443, 0.90296471, 0.91135611, 0.88797021])}'파이썬 > 머신러닝' 카테고리의 다른 글
| 머신러닝 다중클래스 분류 모델 예측 평가 및 성능 시각화 (0) | 2022.11.24 |
|---|---|
| 머신러닝 기본 회귀 모델과 기본 분류 모델의 평가방법 - score(), predict() (0) | 2022.11.23 |
| 모델 평가란? 로지스틱회귀에서 KFold 교차검증 사용해보기 (0) | 2022.11.21 |
| 넘파이numpy 와 서킷런sklearn을 활용한 데이터 이상치 확인 및 해결 (0) | 2022.11.17 |
| 서킷런 sklearn으로 수치형 데이터 전처리 [스케일링 - 표준화, 로버스트, MinMax, 정규화] (1) | 2022.11.16 |


댓글