딥러닝 신경망의 기본 구성 요소

1. 인공뉴런과 생물학적 뉴런의 표현법 차이¶

개념적으로 바뀌는 건 없지만, 로지스틱 회귀 모델을 인공 뉴런으로 사용할 때는 세타 값들을 조금 다르게 표현한다.

입력 변수와 곱해지는 세타 값들을 가중치, 영어로는 weight라고 부르고요. 변수로는 weight의 가장 앞 알파벳 $w$를 사용해서 나타냅니다. 그리고 항상 1과 곱해지는 상수 세타는 편향, 영어로는 bias라고 부르고, 변수로는 bias의 가장 앞 알파벳 $b$를 사용해서 나타낸다.

2. 인공 신경망 : 수많은 인공 뉴런이 엮여 있는 모델¶

인공 신경망은 수많은 인공 뉴런을 엮어서 예측하는 알고리즘이다. 동그라미 하나는 인공 뉴런 하나를 나타내고, 선 하나는 각 가중치를 의미합니다. 그리고 편향은 뉴런 안에 있다.

• 가중치(파라미터) : 입력의 중요도를 나타내는 것
• 인공 뉴런 : 퍼셉트론이라 불린다. 입력값과 가중치, 편향을 이용해 출력값을 내는 수학적 모델이다.
• 편향 : 활성화의 경계가 원점으로 부터 얼마나 이동할지를 결정하는 것

 

- 신경망 층과 계산¶

신경망에는 수많은 뉴런들이 있지만, 보통 여러 뉴런들을 '층' (뉴런들의 열 하나가 하나의 층)이라는 단위로 묶어서 표현한다.

가장 앞에 있는 층의 뉴런들은 입력 변수, 이미지의 경우 한 이미지의 총 픽셀 데이터들이 들어오는 뉴런들이고, 이 층은 입력층이라고 부른다.

입력층 뉴런들은 데이터를 따로 처리하지는 않고, 인풋 데이터를 그대로 출력값으로 갖게된다.

나머지 층 뉴런들은 모두 로지스틱 모델들이다.

 

로지스틱 모델은 인풋을 받아서 가중치와 편향을 사용해서 처리한 다음 시그모이드 함수에 처리한 값을 넣어서 0~1 사이의 숫자를 리턴한다. 신경망에서 각 뉴런의 인풋은 바로 전 층 모든 뉴런들의 출력이다.

전 층 뉴런들의 출력을 벡터 xx, 뉴런 하나의 가중치들을 ww, 편향을 상수 bb로 표현한다면, 뉴런의 출력은 아래의 수식처럼 계산해볼 수 있다.

 

뉴런의 출력을 계산하기 위해서는 전 층의 출력을 미리 다 계산해놔야 되고, 뉴런의 출력은 항상 층 단위로 계산된다.

 

[요약]

1. 먼저 입력층에서 인풋을 받아서, 다음 층 모든 뉴런들의 출력을 구한다.

2. 구한 뉴런들의 출력을 사용해서 다음 층 모든 뉴런들의 출력을 계산 또 뉴런들의 출력을 사용해서 마지막 층 모든 뉴런들의 출력을 계산 마지막 층은 최종 출력이 나오기 때문에 출력층이라고 부르고, 출력층에는 분류하려는 숫자의 개수만큼의 뉴런이 있. 이 뉴런들은 각각 0~9 사이의 숫자 분류 중 하나에 대한 로지스틱 모델을 나타낸다.

3. 입력층과 출력층 사이에 있는 층들은 데이터가 들어가는 층과 나오는 층 사이에 숨어있다고 해서 은닉층이라고 부른다.

- 학습¶

로지스틱 회귀 모델의 목적이 데이터에 가장 잘 맞는 파라미터 세타 값들을 찾아내는 것인 것처럼, 인공 신경망의 목적도 주어진 데이터에 잘 맞는 가중치와 편향들을 찾아내는 것이다.

예를 들어 가중치와 편향을 잘 정해서, 5를 나타내는 이미지의 픽셀 데이터를 인풋으로 넣었을 때, 5에 해당하는 뉴런의 출력은 최대한 1에 가깝게 활성화되고, 나머지 뉴런들은 최대한 0에 가깝게 활성화되게 하는 것이다.

 

9를 나타내는 이미지의 픽셀 데이터를 인풋으로 넣었을 때는, 9에 해당하는 뉴런의 출력이 최대한 1에 가깝게 활성화되고, 나머지 뉴런들은 최대한 0에 가깝게 활성화되게 한다. 잘 맞는 가중치와 편향을 찾는 걸 '신경망을 학습한다'라고 표현한다.

- 예측¶

신경망 입력층에 데이터를 넣어서 마지막 층 뉴런까지 출력을 계산하면 가장 출력이 높은, 가장 많이 활성화되는 뉴런이 있다. 그럼 그 뉴런이 나타내는 숫자로 예측하면 된다.

 

3. 신경망 요소 표현 정리¶

- 층¶

신경망에서 층은 입력층을 제외하고 첫 번째 은닉층부터 센다. 입력 변수는 받아들이는 입력층은 0번째 층이고 그 뒤로 첫 번째 층, 두 번째 층... 이다. 신경망 안에 있는 총 층수는 입력층을 제외한 나머지 층들의 개수이다.

- 뉴런의 출력¶

뉴런은 신경망을 이루는 가장 기본적인 단위입니다. 뉴런의 출력은 뉴런이 얼마나 활성화되었는지를 나타내고, 전 층 뉴런들의 출력, 그리고 자신의 가중치와 편향을 써서 계산된. 뉴런의 출력은 활성을 뜻하는 activation의 가장 앞글자 a를 사용해서 나타낸다.

신경망 안에는 수많은 뉴런이 있기 때문에 각 뉴런의 출력을 서로 구별할 방법이 필요한데, 뉴런의 출력은 몇 번째 층에 있는지 그 층 안에서 위에서 몇 번째에 있는지 이 두 가지로 구별된다. 뉴런이 몇 번째 층에 있는지는 알파벳 a 오른쪽 위에 대괄호 안에 써서 표시하고, 그 층 안에서도 위에서 몇 번째에 있는지는 오른쪽 아래 써서 표시한다.

 

-가중치¶

가중치는 뉴런의 출력을 계산하는 데 사용되는 요소, 전 층 뉴런들의 출력과 곱해지는 값이다.
가중치를 뜻하는 영어 단어 weight의 앞 알파벳 w를 사용해서 나타낸다.

신경망 안에는 많은 가중치들이 있기 때문에 서로 구별할 방법이 필요하다.

가중치는 어떤 층에 있는지 (두 층 사이를 연결하는 가중치는 뒤 층에 귀속), 앞 층에 몇 번째 뉴런과 연결되는지, 뒤 층에 몇 번째 뉴런과 연결되는지 이 세 가지 기준을 사용해서 구별합니다.

 

- 편향¶

편향도 뉴런의 출력을 계산하는 데 사용되는 요소고, 전 층 뉴런의 출력과 가중치의 곱들과 함께 더해지는 값입니다.
편향을 뜻하는 영어 단어 bias의 앞 알파벳 b를 사용해서 나타낸다.

편향은 온전히 하나의 뉴런에 귀속되기 때문에 뉴런의 출력을 나타낼 때와 똑같은 기준을 사용해서 구별된다.

 

 

4. 퍼셉트론 : 가장 간단한 신경망¶

퍼셉트론은 가장 간단한 신경망이고, 생물학적 뉴런을 대략 본떠 만들어 진것이다. 생물학적 뉴런과 마찬가지로 입력과 출력이 있고 '신호'는 입력에서 출력으로 흐른다. Feed-Forward Network모형의 가장 간단한 형태이며 선형 분류(Linear Classifier) 모형의 형태를 띠고 있다. Input(입력)과 Weight(가중치)가 선형 결합의 형태를 띠는 것을 알 수 있다. 선형 결합의 값에 특정 임곗값의 초과 여부를 판단하는 함수를 적용한다. 이 출력 값이 0보다 크면 1, 작으면 01로 결괏값을 내보내 분류하는 모형을 '퍼셉트론'이라 한다.

임곗값의 초과 여부를 판단하는 함수를 활성화 함수(Activation Function)라한다. 가장 기본적인 Activation 함수는 Step Function으로 Input 값이 0 이상이면 1, 이상이 아니면 0을 출력하도록 하는 함수이다.

퍼셉트론은 처음에 가중치를 랜덤하게 설정한 후 모델의 에러와 가중치를 개선해 나간다. 학습 규칙에 따라 가중치가 업데이트 되고, 모든 데이터를 올바르게 분류 할 때까지 이 과정을 거친다.

 

 

퍼셉트론 유닛에는 입력(x), 출력(y)과 3개의 다이얼이 있다.

가중치(w), 절편(b), 활성화 함수(f)이다.

• 활성화 함수 : 신경망과 타깃 출력을 기반으로 설계자의 직관에 따라 결정된다.

→ y=f(wx+b) - 출력 = (가중치*입력+절편)

일반적으로 퍼셉트론에는 입력 하나 이상 사용한다. 이런 일반적인 상황을 벡터로 표현할 수 있다. 즉 x입력과 w가중치은 벡터고 x입력과 w가중치의 곱셉은 접곱(dot procuct)로 바뀐다.

→ y=f(wx+b)

f 표시한 활성화 함수는 일반적으로 비선형 함수이다. 선형 함수는 그래프가 직선인 함수이다. 즉 퍼셉트론은 선형 함수와 비선형 함수의 조합이다.

 

 

5. 다층퍼셉트론 MLP : Multi Layer Perceptron¶

퍼셉트론이 지니고 있는 한계점을 극복하기 위해 여러 Layer를 쌓아올린 Multi Layer Perceptron이 등장하게 되었다. 퍼셉트론 Input과 Output Layer(입력층과 출력층)만 구성되어 있지만, MLP는 중간에 Hidden Layer(은닉층)을 넣은 형태이다.

Input Node 세개와 Hidden Layer의 가장 윗 노드와 연결한 모든 선을 하나의 퍼셉트론으로 볼 수 있다.

MLP의 Hidden Layer(은닉층)는 여러 퍼셉트론의 조합으로 볼 수 있고 이들의 조합이 Output Layer(출력층)로 연결된다. → MLP는 여러 개의 퍼셉트론 조합과 이것들의 재조합으로 복잡한 비선형적인 모형을 만들어내는 것이라 할 수 있다.

딥러닝의 기본 구조가 되는 것이 신경망이라면 기본적으로 MLP를 의미한다. MLp의 Hidden Layer를 쌓으면 층이 깊어지기(Deep) 때문에 딥러닝의 기본적인 모델이 된다.

비선형은 Input 1개, Hidden 1개, Output 1개, 즉 총 3개의 Layer로 연결되어 있는 MLP이며 각 원은 노드(Node)라고 부른다. Input Node의 수는 Input Data의 변수의 수가 되며 Hidden Layer와 Hidden Node의 수는 사용자가 지정해야 할 하이퍼파라미터이다. 출력층은 최종적으로 모델의 결괏값을 의미하기 때문에 Output Node의 수는 1,0 부터 9까지의 숫자 분류를 하고자하는 경우 Output Node의 수는 1,0 부터 9까지의 숫자 분류를 하고자 하는 경우 Output Node의 수는 10이 된다.

 

 

6. Feed Forward : 순전파¶

신경망은 Input에서 가중치는 은닉을 거쳐 Ouput을 보낸다. 이과정을 'Feed Forward'라 한다.

순전파는 입력층으로 들어오는 정보가 층 단위로 마지막 층까지 계산되는 과정을 의미. 신경망은 출력층 뉴런들의 출력을 사용해서 예측하기 때문에 순전파는 굉장히 중요한 개념이다.

- 뉴런 출력 계산¶

입력층을 제외한 신경망의 모든 층의 뉴런들은 출력을 전 층 모든 뉴런의 출력과 가중치와 곱한 후, 편향과 함께 모두 더한 z를 계산하고 계산한 z를 시그모이드 활성 함수에 넣어서 계산한다. 입력층의 출력은 그냥 받아들이는 입력 변수 그대로 사용한다.

- 순전파 전체 과정¶

순전파는 첫 번째 층부터 시작해서, 마지막 출력층까지 층 단위로 위에서 배운 내용을 모두 계산하는 과정이다.

 

7. Back Propagation : 역전파¶

Feed Forward를 이용해 Input에서 Output까지 계산한다.

여기서 Output은 우리가 얻고자 하는 예측 값을 의미한다.

그리고 모델(신경망)의 예측 값과 실제 값의 차이(Error)를 계산한다. 이 에러를 바탕으로 신경망의 가중치들을 업데이트한다. 뒤의 가중치(가중치2)부터 업데이트 하고 이후에 앞의 가중치(가중치1)를 업데이트 한다.

순전파를 이용해 계산된 에러를 바탕으로 뒤의 가중치부터 업데이트한다고 해서 이 과정을 역전파라 한다.

Propagate라는 단어는 전파하다라는 뜻으로, Back Propagation는 에러를 뒤에서 부터 전파하겠다라는 의미이다.

순전파와 역전파를 계속 반복하며 가중치를 업데이트하며 점차 신경망의 Output(예측 값)이 실제 값에 가까워지면서 모델의 학습이 이루어진다.

여기서 데이터를 여러번 순전파와 역전파를 반복하며 학습하는데, 이반복하는 횟수를 에포크(Epoch(세대))라고한다.

(*100 에포크라고 하면 전체 데이터셋에 대해 100번의 순전파와 역전파를 했다고 이해하면 된다.)

 

❓배치(batch)와 에포크(epoch) 

컴퓨터의 메모리는 한정되어 있기 때문에 모든 데이터를 한번에 처리할 수 없다.
따라서 전체 데이터를 나눠서 학습하게된다. 이때 떼어서 학습하는 단위가 '배치'이다.
배치크기 만큼 학습하여 전체 데이터 모두를 학습하면 '1에포크'를 학습했다고 부른다.
100에포크를 학습한다하면 이때 학습한 반복 횟수를 이터레이션이라고 부른다.

[요약] : 컴퓨터의 메모리 (한정) -> 한번에 처리 X -> 전체 데이터를 나눠서 학습 (학습하는 단위 ; 배치(batch))

* 배치(batch) : 딥러닝 모델의 가중치(손실 보정)를 업데이트시킬 때 사용되는 데이터의 묶음 단위
* 에포크(epoch) : 배치 크기 단위로 전체 데이터 모두를 학습하는 단위 = 배치 X 이터레이션
* 이터레이션(iteration) : 1에포크를 완성시키는데 필요한 배치의 반복횟수

 

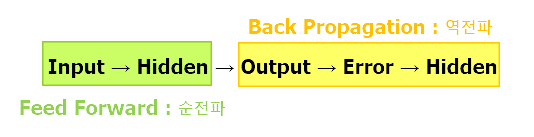
이 내용을 정리하면 신경망의 Input → Hidden → Output 까지는 데이터에서 예측값을 계산하는 순전파(Feed Forward) 과정이고, Ouput에서 에러를 계산해 Weight를 업데이트하는 과정을 역전파(Back Propagation)과정이라 한다.